| 地球是不规则的球体,其表面凹凸不平,形态复杂,不能用简单的数学公式来表达和计算,也不能直接作为测量与制图的基准面,因此,需要寻求一种与地球自然表面充分接近的规则曲面,来代替地球自然表面。假想海洋在无风、无浪、无潮汐的静止状态下穿透大陆,形成处处与铅垂线相垂直的封闭曲面,这个曲面被称为大地水准面,它是一个没有褶皱、没有校角的连续封闭曲面。 大地水准面是一个与重力线方向处处垂直的重力等位面。由于地球内部质量分布的不均匀性,导致重力场分布不规则,因此大地水准面呈现为一个不规则的曲面。在实地测量工作中,大地水准面被视为野外作业的基础面,同时也是高程计算的起始面。然而,理想状态的大地水准面在现实中是无法精确获得的,因此通常我们会采用平均海平面或似大地水准面作为替代。似大地水准面是通过从地面点沿正常重力线测量正常高,并将这些点连接成一个封闭的曲面而得到的。 
在18世纪中叶之前,人们主要依赖弧度测量法来探索地球的形状。1743年,法国的克莱洛提出了一种设想,认为地球的外表面应是一个水准椭球体,即椭球表面上的所有点具有相等的重力位。到了1828年,德国的高斯进一步定义了大地水准面,将其描述为与全球平均海面最为接近的重力等位面。1873年,高斯的学生利斯廷引入了“大地水准面”这一术语,用以具体描绘高斯所提出的数学模型。直至20世纪中叶,人们才开始尝试通过重力测量方法来精确确定大地水准面。然而,由于当时全球重力数据的稀缺,主要依赖天文重力推算,所得结果的精度仅为米级。自20世纪80年代以来,随着地面重力数据的日益丰富,卫星跟踪技术的不断进步,以及卫星测高技术的出现,全球及区域大地水准面的精化工作在全球范围内得到了广泛的开展。 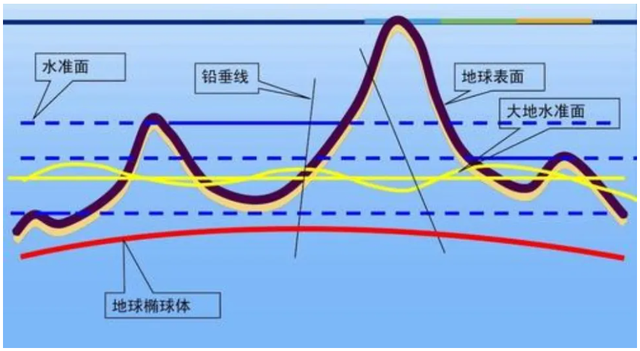
利用地球重力场模型可确定大地水准面,所以有时也将重力场模型称为大地水准面模型。美国科学家库拉于1966年首次建立了8阶地球重力场模型,美国先后研制了JGM、OSU系列模型、360阶EGM96模型、2160阶EGM2008模型。EGM2008模型空间分辨率为5’×5’,精度约20厘米。我国在20世纪50至70年代,形成了第一代似大地水准面CQG60和CQG80,总体精度为3~10米;2000年推出我国首个陆海统一重力似大地水准面CQG2000,空间分辨率为5’×5’,精度约0.4米;似大地水准面CNGG2015的空间分辨率为2’×2’,精度达9.3厘米。最新的重力似大地水准面精度有望达到5厘米,可大大拓展卫星定位在精密高程测量中的应用。
|

